The proof behind The Man Who Knew Infinity

Srinivasa Ramanujan was a genius, but he needed help to prove it
Published 7 May 2016
Since the success of A Beautiful Mind depicting the life of John Nash, the ‘historical mathematician biopic’ has been popular lately.
The lives of Stephen Hawking and Alan Turing were covered in The Theory of Everything (2014) and The Imitation Game (2014). Combined with hugely popular science-fiction movies that take the science seriously, like The Martian, Gravity and Interstellar, it’s a good time to be a scientist and a movie-lover.
The latest maths biopic is The Man Who Knew Infinity, about Indian mathematics genius Srinivasa Ramanujan (Dev Patel), who shocked and surprised the English mathematical establishment at the start of the 20th century by the depth and originality of his research in additive number theory.
Ramanujan visited Trinity College in Cambridge during 1914-1919 to collaborate with G. H. Hardy (Jeremy Irons) and, to a lesser extent, J. E. Littlewood (Toby Jones), and died soon after from the effects of tuberculosis.
While less well known by the average moviegoer than Alan Turing or Stephen Hawking, among mathematicians Ramanujan’s is a famously romantic story about a man in love with numbers who finds early companions in Hardy and Littlewood and later earns the respect of all.
The Man Who Knew Infinity does an excellent job at portraying mathematicians as human beings with all their virtues and faults. It respectfully approaches the quest of two men (Hardy and Ramanujan) to solve one of the most challenging mathematical problems of the era, but more on that later.

Most of the story takes place on the hallowed grounds of Trinity College, and besides mathematical struggles the film also depicts bitter rivalries and politics within the academic ranks.
But we have seen all of that before and those not familiar with the depth and beauty of Ramanujan’s mathematics may leave the cinema feeling somewhat unfulfilled. The pace of the movie is slow and one wonders whether, without the mathematics, there is enough content for a feature film. Not that the movie is a waste of time – both Irons and Patel are convincing in their roles and skilfully develop a deepening tension between Hardy and Ramanujan.
At the time, Ramanujan’s results were astounding as he was self-trained and virtually unknown in professional circles. Moreover his style was very enigmatic as he commonly just stated his results without explanation or any kind of proof. Nevertheless, as Hardy famously remarked:
(The results) must be true, because, if they were not true, no one would have the imagination to invent them.
A major theme of the movie is this idea of a mathematical ‘proof’. Hardy repeatedly emphasises the importance of providing logically sound arguments and proofs of mathematical statements, at times almost belittling Ramanujan for his lack of mathematical rigour.
As he explains, in this way one can be sure that statements are true beyond mere examples, and indeed can be trusted to be true forever. It comes as a shock to Ramanujan when Littlewood notices that his argument for deducing the prime number theorem is flawed, and this moment opens his eyes to the nuances of the mathematical proof.

Director Matthew Brown has gone out of his way to make sure that the mathematics in The Man Who Knew Infinity is depicted truthfully. Formulas that made it to the screen, and luckily there are a few, are correct and carry meaning. To our taste there could have been a bit more time spent on explaining mathematical ideas, rather than just flashing formulas, but we accept that the general public is probably not ready for that yet.
The mathematics of ramanujan
To illustrate some of Ramanujan’s work, we start with a famous result in mathematics, the geometric series:

where the Σ symbol denotes that the sum must be taken over all terms of the form xn where n runs over the integers between 0 and ∞. The statement is that
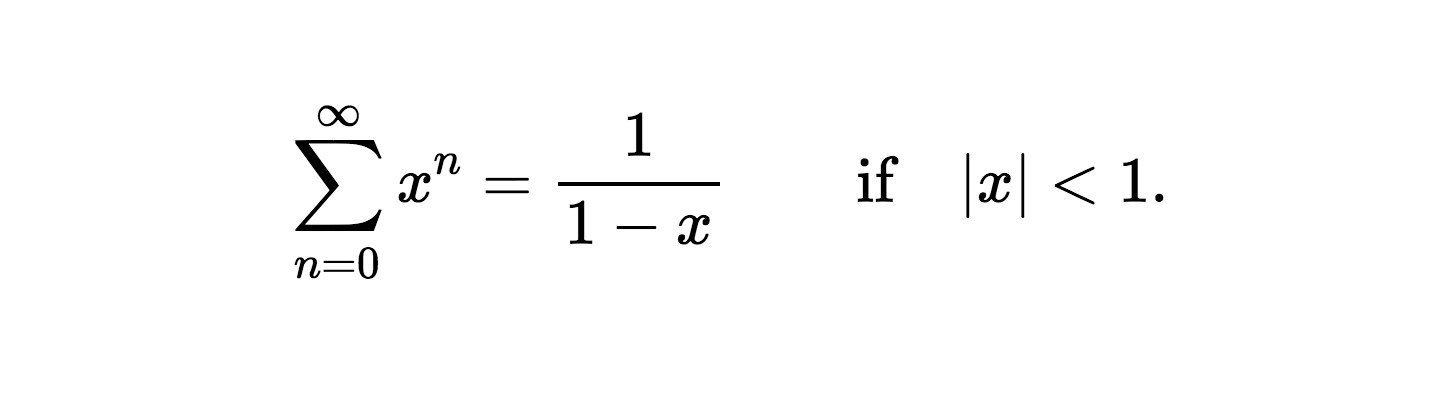
The left hand side of the equation is more like a definition, we cannot practically add together one-by-one an infinite amount of numbers. The right hand side is what we call a `closed form’ expression, and allows us to easily calculate the exact answer for the infinite sum for any value of x. We provide a proof for this statement below.

Partitions
One of Ramanujan and Hardy’s achievements, cited many times in The Man Who Knew Infinity, is a formula for calculating the number of partitions for any integer. In mathematics, a partition is a way of writing a number as a sum of positive integers (called parts), such as
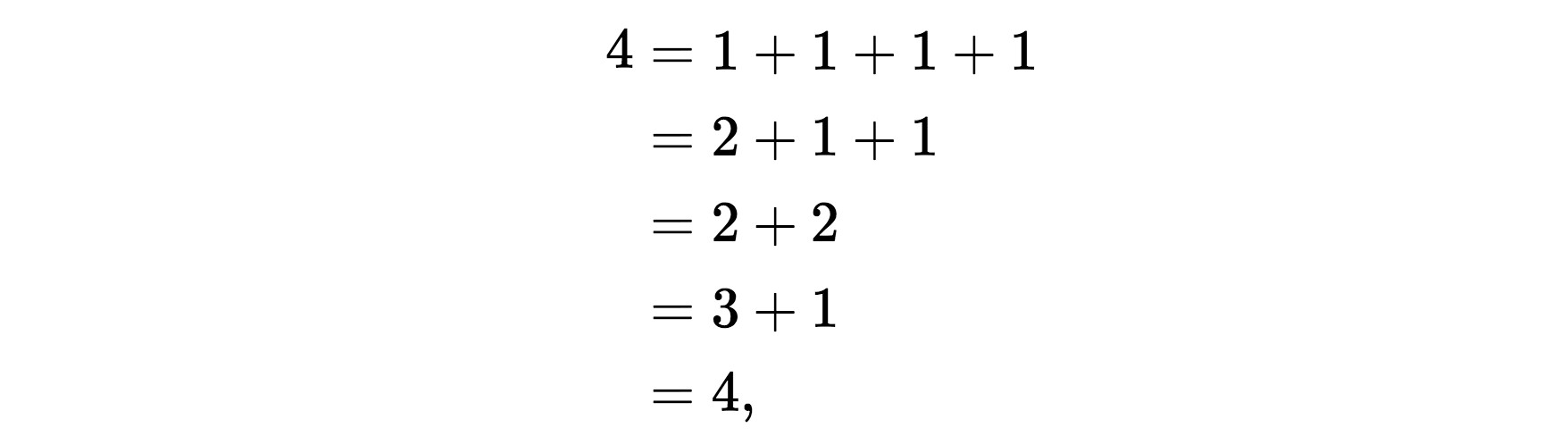
and so there are five ways to partition the number 4. Another mathematical giant, Leonhard Euler, gave an implicit formula for P(n), the number of partitions of n. In the example above, P(4)=5. Euler’s formula used an infinite product,
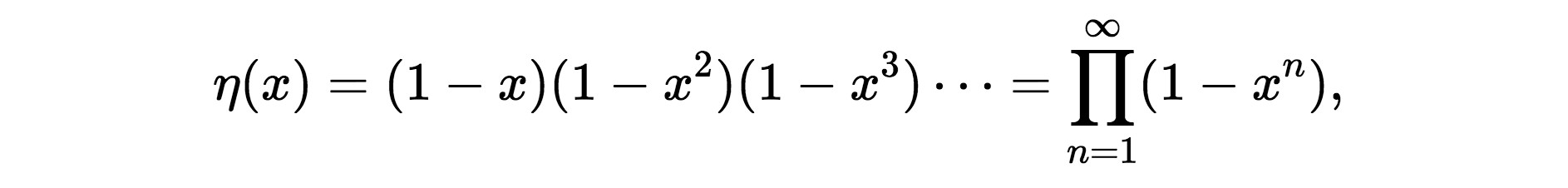
where the Π symbol means that you need to multiply all factors of the form 1 − xn where n runs from 1 to ∞. Euler’s formula can be rewritten by taking the reciprocal of η(x) and then writing it as a sum of powers of x:
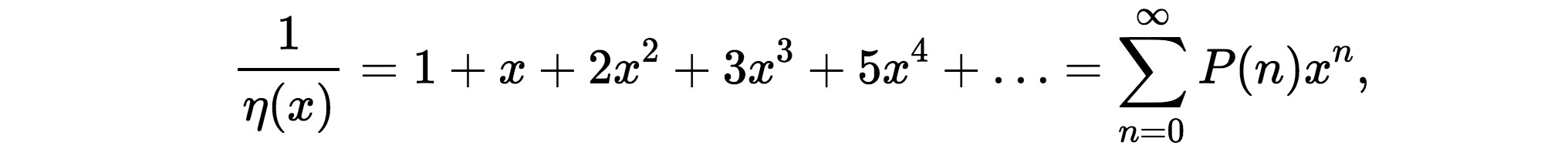
where now the coefficients in the infinite sum are not equal to 1 as in the geometric series, but given by P(n). The formula above determines P(n) implicitly but it was thought impossible to find a `closed form’, or explicit expression for P(n). Remarkably, Hardy and Ramanujan managed to do exactly that, during their brief but intense collaboration. Against all odds they found a very precise formula for P(n), which is too complicated to give here in full. We state only their asymptotic result, namely that for large integers n, the number P(n) is well approximated by
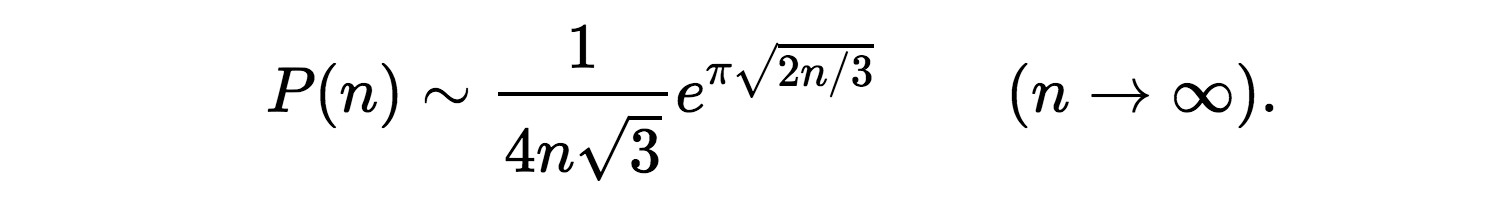

Mathematical proof of the geometric series
While it would be unreasonable to write out Hardy and Ramanujan’s complex proof in this space, we can give an (oversimplified) example of the kind of reasoning they went through by showing the proof to the geometric series, stated above. To prove the statement
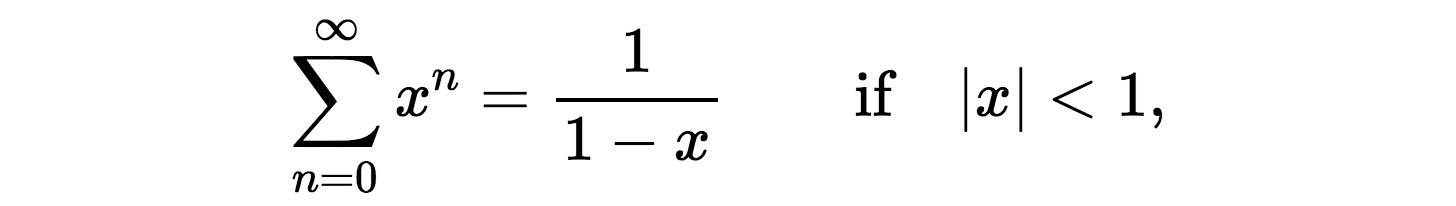
we first consider a finite sum, including m+1 terms. For example, for m=3 we get
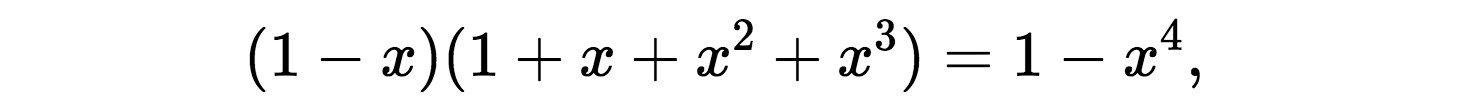
which follows from expanding and then simplifying the left hand side of the equation. We can generalise this for any number m:
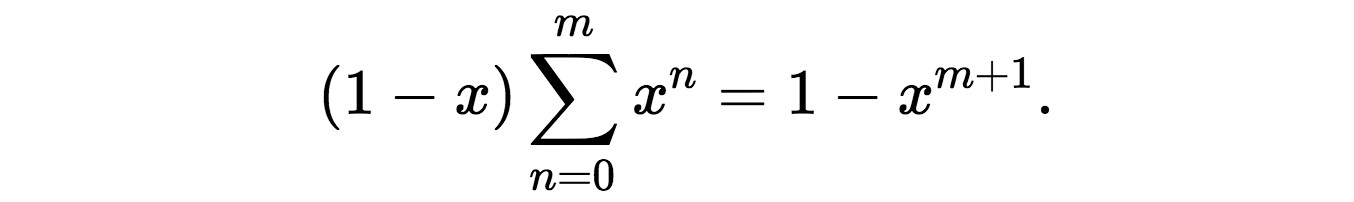
If |x| < 1 then it is possible to take the limit m → ∞ in which the term x(m+1) goes to zero and in this way we prove the result for the infinite sum.
The proof of Hardy and Ramanujan of their formula for P(n) is complicated, and few professional mathematicians have examined and appreciated all its intricacies. Nevertheless, due to their work (and that of others to follow) we now have very explicit information about the value of P(n) for any n. And because they gave us a proof, we will never have to doubt this result.
Banner image: Warner Bros.

