What maths can tell us about the spread of the new coronavirus

Since officially recognising the outbreak of a new coronavirus (2019-nCoV) governments around the world have acted swiftly to try and limit its spread, shutting down transport both in affected regions in mainland China and internationally.

Two key questions are then whether these measures will be sufficient to contain the outbreak in China itself, and whether the virus’ importation to other countries will result in further localised spread.

Mathematics can help us to answer these questions.

In the early stages of any outbreak, particularly one caused by a previously unseen virus, there can be considerable uncertainty around how contagious a virus is, how quickly it will spread, and how effective control measures may be.

In the case of the new coronavirus, mathematical modelling is playing a key role in interpreting early epidemiological data on the outbreak.

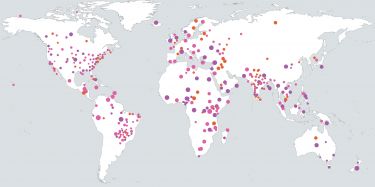
It was mathematical modelling based on airline passenger numbers and the number of infected people detected outside China that gave us early estimates of the size of the outbreak in the city of Wuhan.

Similarly, modelling was used to quickly identify which countries were most at risk of experiencing imported cases, accurately predicting almost all countries that now have cases of the virus.

Models have also been made available as interactive tools to help authorities ascertain likely patterns of global spread, and whether border screening would be effective in detecting imported cases.

So, what does the mathematics say about how fast this outbreak may spread?

The two key factors that determine how quickly a disease will spread are:

1. The average number of people a single person is likely to infect; and

2. How long it takes for these infections to happen.

The average number of secondary infections, known as the reproduction number, is termed “R0” when it applies to a population where everybody is susceptible to infection.

This circumstance is rare and applies only to a new bacteria or virus (like this one) to which the population has no immunity from past infections or vaccination.

Several teams around the world have used models to estimate R0 from available case data. Depending upon the methods used, estimates of R0 for the new coronavirus have ranged from 1.3 (similar to seasonal influenza) up to 3 or 4 (similar to SARS).

The time between onset of an initial infection and a second person becoming infected is called the “serial interval”. Early estimates indicate that the new coronavirus has a serial interval of around seven days, which is substantially longer than for influenza which sits at around three or four days.

So even if the new coronavirus has a higher R0 than seasonal influenza, it may spread more slowly.

While R0 and the serial interval can tell us a lot about how the virus spreads, they don’t tell us everything we need to know about how large an outbreak might be and how difficult it could be to control.

The severity of symptoms caused by this disease will be another key factor that determines whether the outbreak can be contained.

Paradoxically, while it may seem that a more severe disease would be of greater concern, it may actually be easier to control. When symptoms are severe, infected people are more visible, making them easier to identify, quarantine and treat.

In fact, people experiencing severe symptoms are more likely to reduce their contact with others, so reducing the rate at which they spread infection.

At this point, we know that the new coronavirus can cause severe disease in at least some cases – notably older people with pre-existing health conditions. It appears to cause only mild symptoms in many other cases, with very few reported cases in children and infants.

Using models, we can explore a range of possible “what if” scenarios around both the transmissibility and severity of a virus in order to assess how fast it might spread, how visible it may be and our chances of bringing it under control.

Much like fighting a bushfire before it gets out of control, an early response to an outbreak is much more likely to succeed in containing its size and the damage it causes.

On 23 January, China introduced travel restrictions affecting 20 million people, later extending these to affect 50 million people – an unprecedented scale of response.

These restrictions may have come too late to prevent the spread of the outbreak to other parts of China, but there is still hope that they may help limit global transmission.

However, models of past outbreaks suggest that while travel restrictions may delay the spread of an outbreak, they have less effect on reducing its size.

There is currently no vaccine against this coronavirus, but the Coalition for Epidemic Preparedness Innovations is funding three laboratories around the world (one in Queensland) to make one.

The recent isolation of the novel coronavirus at the Peter Doherty Institute for Infection and Immunity has been an important step in supporting these efforts.

As the characteristics of a potential vaccine become better known, mathematical models can be used to explore alternative scenarios about effectively distributing a vaccine in order to limit transmission and protect the most vulnerable population groups.

Strategic use of a vaccine is particularly important in the early stages, when only limited quantities may be available.

In Australia, enhanced surveillance measures will be put in place as more cases emerge in an attempt to characterise the spread of virus – these are known as First Few Hundred (FF100) studies and aim to collect data from households with confirmed cases.

The smaller number of possible contacts, and the ability to closely monitor all residents within a household, should provide much more accurate data about symptom onset times in individuals and asymptomatic cases.

The challenge is that specialised models and methods are required that account for the inherent randomness in the spreading process.

As new information emerges during an outbreak, the assumptions and data that feed into models are updated, leading to a constant revision of estimated risks, impact and controllability.

There will always be uncertainties both in the data captured during an outbreak and the estimates generated by models.

It is crucial that these uncertainties are clearly communicated in a way that supports decision making, rather than causing indecision.

Decision makers must also balance a broad range of social, political and ethical considerations when deciding how best to respond to an outbreak.

Algorithms and tools for supporting decision making can help to synthesise the output from mathematical models with other sources of information to provide coherent and timely recommendations under conditions of high stress and uncertainty.

Banner: Getty Images